Suma A Doi Vectori Formula

Vectori vectori in plan adunarea vectorilor regula triunghiului regula paralelogramului pentru suma a doi vectori definiţie. Fie doi vectori liberi ca cei din figura de mai jos. Utilizand relatia 14 se obtine pentru diferenta a burmatoarea expresie.

coreldraw graphics suite 2018 trial download corpuri de iluminat dormitor copii care se joaca credit ipotecar bt calculator crucea de pe caraiman romania credit ifn pentru restantieri culegere limba romana clasa 4 culegere admitere medicina umf carol davila biologie 2017 pdf

Operatii Cu Vectori Adunarea Vector2 Youtube

Suma Si Diferenţa Vectorilor Plus Educational

Produsul Scalar A Doi Vectori 7 2 Pg4 Youtube

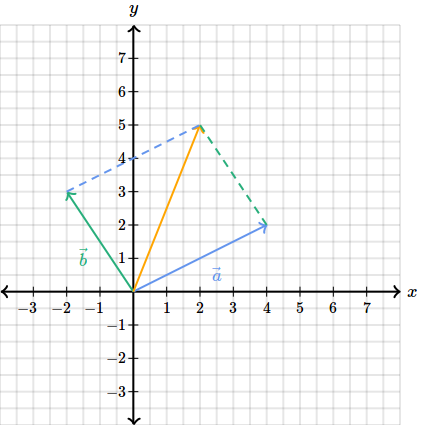
Operatii Cu Vectori Si Coliniaritatea A Doi Vectori

$Operatii Cu Vectori Si Coliniaritatea A Doi Vectori$

Un mod de a intelege acest rezultat este sa ne gandim la diferenta dintre doi vectori drept o suma.

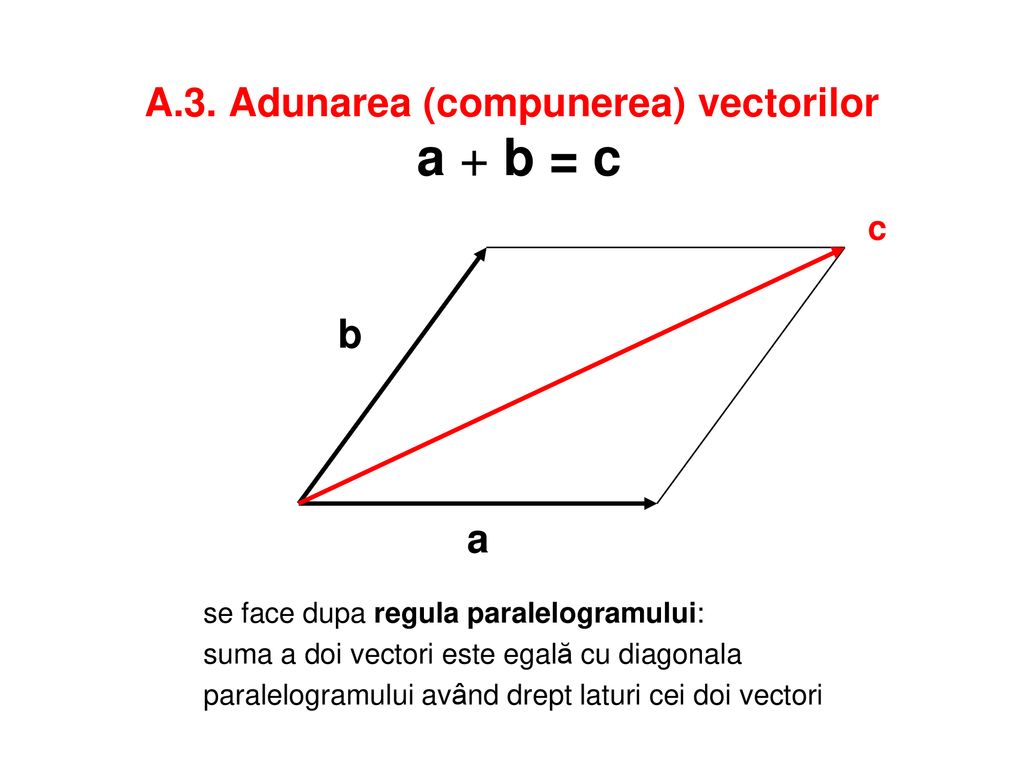
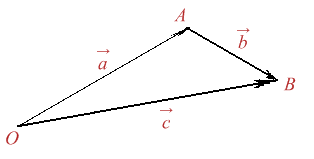
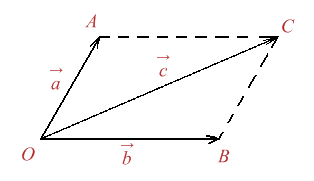
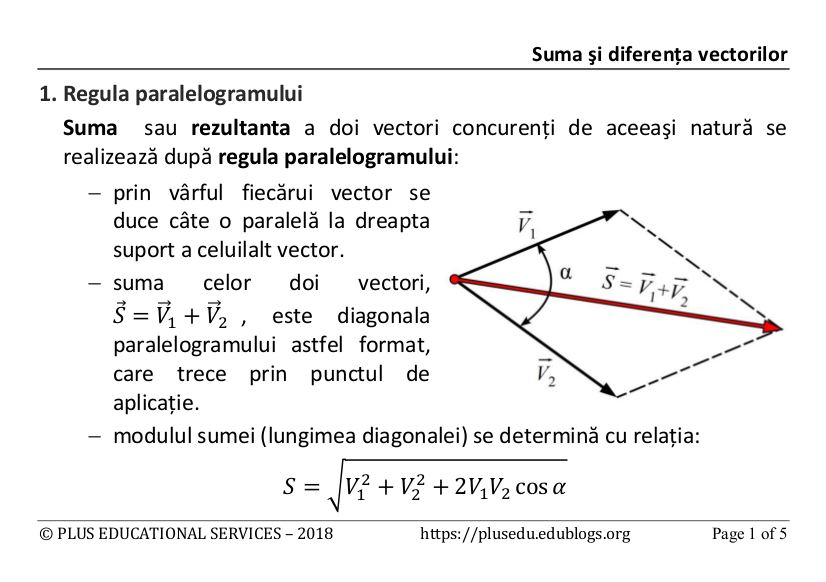
Suma a doi vectori formula. 14 astfel componentele vectorului c pe cele trei directii se obtin prin sumarea componentelor vectorilor asi bpentru fiecare directie in parte ci ai bi unde i x y z. Suma a doi vectori si înmul tireaunuivectorcuunscalar fiind da ti doi vectori suma lor se deﬁne ste ajutorul reprezentan tilor astfel. Cei doi vectori formează unghiul orientat unghi a cărui măsură o notăm cu. Deﬁnitia 2 1 5 daca asi bsunt doi vectori având reprezentan tii oarespectiv abatunci suma a bare reprezentantul ob conform ﬁgurii de mai jos.

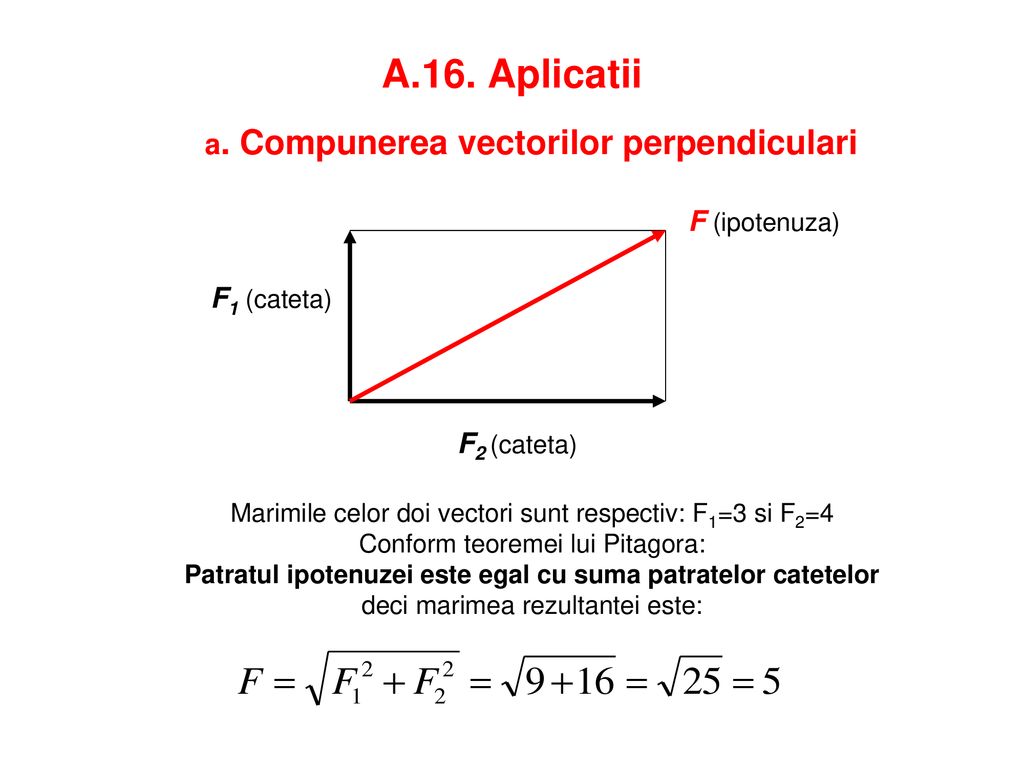
Expresia analitică a unui vector. V 1 v 2 x 1 x 2 i y 1 y 2 j produsul unui vector cu un scalar. Vectori vectori in plan adunarea vectorilor regula triunghiului regula paralelogramului pentru suma a doi vectori definiţie. V 1 v 2 x 1 x 2 y 1 y 2 v 1 v 2 v 1 v 2 c o s v 1 v 2 modulul lungimea unui vector u a i b j este u a 2 b 2.

Suma a doi vectori. Daca ne avem doi vectori sa spunem a 4 2 a 4 2 si vectorul b 2 3 b 2 3 atunci suma celor doi ar insemna sa adunam numerele care sunt pe acelasi rand. C a b axi ayj azk bxi byj bzk ax bx i ay by j az bz k. Fie vectorii vectorul liber se numeşte vectorul suma al vectorilor dati dupa regula paralelogramului sau a triunghiului.

α v 1 α x 1 i α y 1 j produsul scalar a doi vectori. Fie vectorii vectorul liber se numeşte vectorul suma al vectorilor dati dupa regula paralelogramului sau a triunghiului. Proiectia unui vector pe o axa vectori. Numărul se numește produsul scalar al vectorilor și și este egal cu produsul dintre modulul vectorului modulul vectorului și cosinusul unghiului dintre cei doi vectori.

Pentru a descompune un vector din plan după doi vectori necoliniari și determinăm coeficienții respectiv din suma. A b 4 2 2 3 2 5 a b 4 2 2 3 2 5. A b c a b c a b c a b c. Descompunerea unui vector după doi vectori dați.

Vectori coliniari şi vectori perpendiculari. Formula de calcul pentru lungimea unui vector exprimat cu ajutorul versorilor. înmulțirea unui vector cu un scalar. Pentru a putea face acest lucru vom lua un punct pe dreapta suport a vectorului și vom construim dreptele cu aceleași direcții ca și vectorii respectiv care să treacă prin punctul la fel ca în figura de mai.

Produsul scalar a doi.